 |
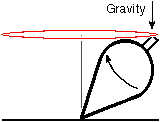
Here is a top. We have spun it clockwise, as shown by the curved arrow, and at an angle so that gravity is trying to twist the axis clockwise (arrow). We know from experience that instead of falling toward the table, the axis of the top will precess about a cone moving the handle around the red horizontal circle centered above the point of contact with the table. Which direction will the handle move about this circle, clockwise or counterclockwise, i.e. in the figure will the handle move toward us or away? Once you understand the reason for this curious response - moving one way when pushed another - you can easily predict which direction the axis will move without resorting to memorized formulas involving vectors and "right-hand" rules, which are too often the refuge of the ignorant. [Feynman says, "many simple things can be deduced mathematically more rapidly than they can be really understoood in a fundamental or simple sense...the precession of a top looks like some kind of a miracle involving right angles and circles, and twists and right-hand screws. What we should try to do is to understand it in a more physical way." (Lectures on Physics, Vol. I, p. 20.6)] |
Stationary Wheel
|
Consider a stationary bicycle wheel on a blue axle suspended by a string on the left. Gravity pushing down (red arrow) and is converted by the force of the string into a torque, transmitted through the spokes, to push the top of the wheel to the right and the bottom of the wheel to the left (violet arrows). Left to its own devices the wheel will flop down in the direction of the torque. The top of the wheel moves to the right and the bottom to the left, as expected. There is no weirdness if the wheel is not spinning. |
|
|
FLOP! |
Spinning Wheel