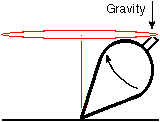
|
1) Which way should the handle of the top in the first figure move - toward the viewer or away? It should move toward the viewer. (Note that the top is spinning in the opposite direction from the bicycle wheel in the illustration. Its surface has the maximum velocity to the right when it is furthest from the viewer.) |
 |
2) Should increasing the torque by adding weight to the axle of the bicycle wheel increase or decrease the velocity of precession?
With greater torque, the acceleration and the right-left rim velocity will be proportionately greater, so rate of precession is directly proportional to torque.This is a key factor in NMR. Increasing the strength of the magnetic field (or changing to a stronger nuclear magnet) increases the precession frequency proportionately.
3) Should increasing the rate at which the bicycle wheel spins increase or decrease the velocity of precession?
Surprisingly enough raising the spinning rate slows the velocity of precession!As a top (or a gyroscope) slows down, it precesses faster.
The reason is that when the wheel is spinning faster there is less time for the torque to generate right-left velocity (the acceleration does not act for as long a time).
For an atomic nucleus the spinning rate is fixed at a constant value, just as its charge or its mass is fixed, so one does not have to worry about this variable in NMR.
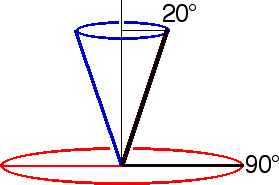
4) The figures above show the axle at 90° to the vertical string. How should setting the axle at other angles influence the rate of precession?
The torque from gravity decreases as the angle deviates from 90°. Since at 0° there is no torque, it will not surprise you to know that the torque is proportional to the sin(a), where a is the angle the axle makes with the string.This reduction in torque would be expected to slow the precession (see Question 2), but there is an offsetting factor:
These two factors, the reduction in
torque and the reduction in necessary angular
reorientation exactly offset one another, so the
precession rate is independent of the angle.
When the axle is at 90° to
the string, its direction must change through 180°
in order to effect a full cycle of precession
(red
circle). If the axle makes a sharp
angle with the string a full cycle of precession requires
only that it change angle slightly to move around a
cone
(blue) with the string its axis.
The amount of reorientation is proportional to the radius
of the base of the cone, which is proportional to the
sine of the angle. Thus the amount of reorientation
needed is proportional to
sin(a).
This is the reason that a nucleus which has a spin high enough to allow several different quantized orientations in the magnetic field has the same precession frequency in each of these levels.
Return to Chem 125 homepage Return to Precession page
copyright 2003 J. M. McBride