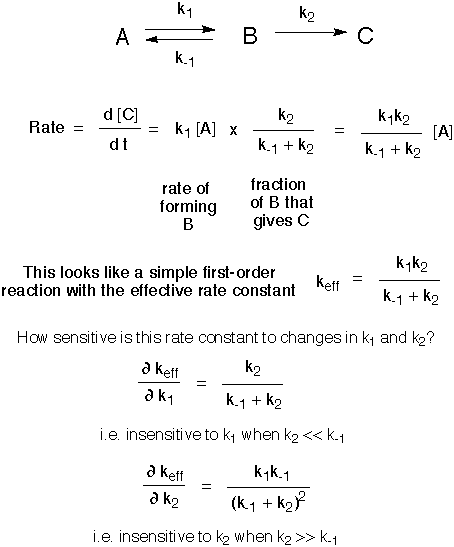
So the reaction rate is mostly sensitive to energy of the higher transition state leading away from B. This slow reaction is called the rate-determining step.
Rate-Determining Steps II. Radical Chain Reaction
It seems curious to begin our study of real chemical reactions by studying a fairly unusual class of reactions, those involving "odd electron" molecules, or free radicals. These molecules that have SOMOs are almost invariably able to achieve stability by reacting with one another, so, except for O2, it is difficult to find them unassociated in the laboratory or in nature. Most reactions we will study involve HOMO/LUMO mixing instead of SOMOs.
As we mentioned in lecture there are three reasons for starting with a brief discussion of radical reactions:
(1) There is a certain aesthetic appeal to designing the synthesis of complex substances starting from the simplest organic molecules, hydrocarbons lacking functional groups. Because they lack functional groups, it is difficult to get a toe-hold on these molecules with HOMO/LUMO reactions, but they are subject to free-radical substitution of halogen for hydrogen. One then has the σ* LUMO of the C-X bond from which to proceed.This alone would be a pretty silly reason to start with free-radical reactions.(2) Free-radical reactions have substantial historical and practical importance.
a) Ironically it was halogenation of acetic acid and related compounds (which we now know to be free-radical chain reactions) that convinced Dumas and his French compatriots to abandon the dualistic "radical" theory in the 1840s.b) The discovery of a stable free radical (triphenylmethyl, reported in 1900) ushered in serious thinking about trivalent carbon, which is a key feature of many organic reactions. 1900 is thus a watershed between the structural studies of 19th Century organic chemistry and the mechanistic studies of the 20th Century.
c) Although it is not strictly "organic" chemistry, no one can dispute the importance of the chlorine-atom chain reaction that destroys ozone in the upper atmosphere.
(3) The dominant reason to begin with radical reactions is because they provide such great illustrations of important mechanistic principles:
a) One can use average bond energies to illustrate the influence of thermodynamic stability on equilibrium. Thus fluorination, chlorination, and bromination of hydrocarbons by reaction with the elemental halogens are conceivable processes, but iodination is impossible, because it is uphill in energy by about 12 kcal/mole.b) Propagation in radical-chain halogenation is a great example of a "multistep" mechanism proceeding by two simple reactions.
c) Free-radical halogenations are great illustrations of how catalysts in tiny amount can facilitate transformations that would not proceed by direct interaction of the principal reagents. The role of small amounts of initiation and termination is clearly seen.
d) What is meant by the rate-limiting or rate-determining step in a catalytic cycle is easy to see in these reactions, and what one learns is generally applicable in understanding other catalytic processes, such as those involving biological catalysts like enzymes.
c) Atom-transfer reactions, such as the abstraction of H from RH by Cl. or of Cl from Cl-Cl by R., allow consideration of likely relationships between equilibrium (the enthalpy change in a reaction step) and kinetics or rate (the enthalpy of activation for the step). This builds a bridge between our understanding of structure and the understanding of transformations that will be the subject of the rest of Chemistry 125. Here we encounter "Hammond's Postulate" and the "reactivity-selectivity principle".
As I wrote the following two sections out, it became clear to me that though they are very interesting and important, the details are definitely not as important for this course as some of the other things we are talking about. So don't get bent out of shape trying to understand them if it doesn't come easily. What I want you to develop is an intuitive feeling for the concept of the rate-determining step, and I thought that for some of you seeing the math might be helpful. If it just looks confusing, forget it.
We already discussed in the abstract a two-step reaction where B, an intermediate between A and C, is less stable that either A or C. Thus as A begins to react, B quickly approaches a low concentration that changes relatively slowly until A is exhausted, despite the fact that a large amount of material is passing through it. That is, at any given time B is being destroyed essentially as fast as it is formed. Since the concentration of B is not changing rapidly, the rate of forming product is the rate of forming B from A times the fraction of B that goes to C. (If this were not true B would accumulate or be depleted.)
The following scheme gives a mathematical demonstration that when the two transition states leading away from B are of different height, the rate of forming C from A is dependent on the higher transition state. Our purpose here is not to memorize the math, it is just to confirm the qualitative ideas that we presented in class.
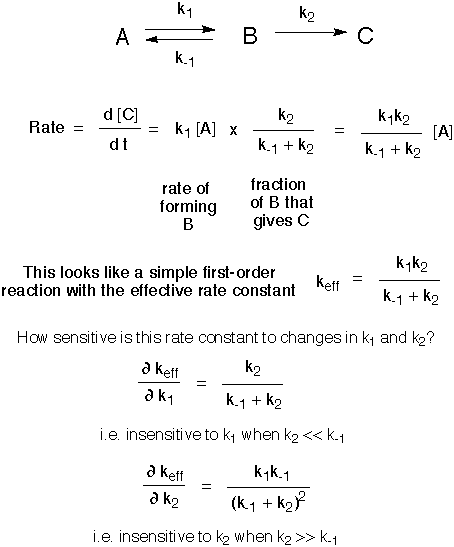
So the reaction rate is mostly sensitive to energy of the higher transition state leading away from B. This slow reaction is called the rate-determining step.
Rate-Determining Steps II. Radical Chain Reaction
Rate determination in a catalytic cycle is actually not so different from that in the consecutive reaction scheme above, the reaction rate is again more sensitive to the rate constant for the slower reaction. Of course there is additional flexibility in the rate constants for this case if one is treating them as pseudo first-order by incorporating the concentration of one of the two reagents ([CH4] with k1 and [Cl2] with k2 in the scheme below). This is shown mathematically below, but what we want to develop is a qualitative understanding of the insensitivity to the rate constant for the faster step, which may at first seem curious.
It may at first seem curious that the rate is relatively insensitive to the rate constant for one of the steps, since cycling of the "machine" requires passing through both steps. The trick is this: the rates equalize by accumulating a larger concentration of the radical starting material for the slower step. Suppose there is 30 times more Cl than CH3 in the scheme below. If one doubles the smaller rate constant k1 (for example by doubling the concentration of CH4, remember this is a pseudo first-order constant), the ratio would change from 30:1 to 15:1, or more precisely ~ 29:2, since the sum of the the two radical concentrations is fixed. This means that the second process (through k2) is going about twice as fast because of the increased concentration of CH3. So, as expected, the machine turns over twice as fast - the first step because of the increased rate constant and the second because of doubling the concentration of CH3.
By contrast, if one doubles the larger rate constant k2, the Cl:CH3 ratio would change by a factor of two in the opposite direction, from 30:1 to 60:1, or better ~30.5 to 0.5. This time the rate of machine turnover hardly changes at all, because the % change in concentration of Cl is negligible, and the increase in k2 is offset by the decreased concentration of CH3. Perhaps a more obvious way of saying this is that there is no room for increasing the concentration of starting material for the slow step appreciably by increasing k2, because practially all of the radicals are in the form of Cl already.

This shows that when k1 >> k2, the rate of product formation is very insensitive to the size of k1. By the same token we could take the derivative with respect to k2 and see that when k2 >> k1, the rate of product formation is very insensitive to the size of k2. In either case calculus shows that the rate is rather insensitive to the size of the larger rate constant, as explained above in terms of the impossibility of increasing the amount of radical waiting for the slower step. When you come to study enzymic catalysis in later life the importance of this fact will crop up again. (Of course one could increase the total amount of radical by increasing the amount of initiation, and then the rate would increase.)