1) Devise a system to give an absolute designation of the chirality of the geometric patterns in the roundels and another system to designate their color-based chirality.
[It is important to note that in devising your systems you must assume that the person with whom you are communicating shares your understanding of "clockwise" or a related concept.]

Obviously schemes like this (e.g. the Cahn-Ingold-Prelog scheme for chemical chirality) are arbitrary in several ways - e.g. what features are used to assign chirality, how they are prioritized, and how names are assigned to the two chiralities - so there is an unlimited number of ways of devising schemes.

One way of assigning geometric chirality in Eadfrith's roundels would use the curves as features and "clockwise" for naming. One might begin tracing the curves near the center and follow their spiral toward the border. In some roundels they spiral clockwise from center to rim, in others they spiral counterclockwise. We might call the ones that spiral clockwise G+ and those that spiral counterclockwise G- (G for geometric).

In assigning color chirality it is necessary to assign priorities.  For example one could assign the colors priority according to their order in the spectrum, red > yellow > green. We might then designate patterns in which decreasing priority proceeds clockwise as C+, and those in which priority decreases counterclockwise as C-.

It would be equally sensible, and equally arbitrary, to trace the spirals from rim to center (like the flow lines of water draining from a sink), or to prioritize colors according to frequency rather than wavelength. These would yield the opposite name in each case. As Prelog pointed out these are just conventions; it is only important that all participants in a conversation agree on the nomenclature to be used. [Interestingly, when one uses four different objects on a 3-D helix (as in the CIP scheme) one obtains the same handedness tracing from high to low priority as tracing from low to high.]

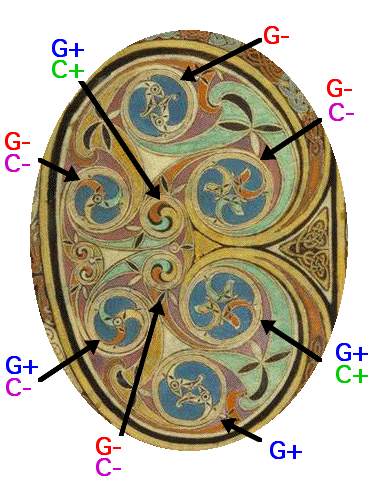
2) Use your two systems to assign chirality to each of the elements in Eadfrith's design and suggest where he made his "mistake". The figure at the right applies these schemes to Eadfrith's roundels:   Clearly Eadfrith aimed to have the top roundels be opposite in chirality to those on the bottom. Geometrically the top blue ones are all G-, and the bottom blue ones are all G+. The small pinwheels in the middle are opposite (top G- / bottom G+). In every case but one the color chirality is the same as the geometric chirality. Probably yellow and green should be exchanged in the bottom left roundel.  Of course we can't know what Eadfrith was thinking, and there are other places in his gospels where "mistakes" are thought to be intentional. 3) Ignoring modest distortions (and his "mistake), is Eadfrith's overall design chiral or "meso"? Neglecting the mistake the overall design is meso. As in meso-tartaric acid, one half is the mirror image of the other. (The symmetry is approximate, because the image is a bit distorted and some roundels are slightly rotated. Note that the same approximation applies at any instant to the isomers of tartaric acid, because their atoms are vibrating.)

4) Consider the knot in the triangular opening at the right of the q (enlarged right). How does Eadfrith show its three-dimensionality? Is the knot symmetrical? Is it chiral? Although the roundels are all two dimensional, Eadfrith shows the third dimension of the knot by breaking lines when they pass under other lines. Corresponding parts of the top and bottom of the knot have the same value of the X-coordinate, but opposite values of Y and Z. Changing the sign of two coordinates leaves the handedness unchanged, so the top and bottom are of the same chirality. The knot is not meso, instead it is chiral and has rotational symmetry about the X-axis (like a propeller).  Since the roundels in question 3 are two-dimensional, the sign of their Z-coordinate is undefined. Their symmetry involves retaining the value of the X-coordinate, but changing that of Y. With only two dimensions one cannot distinguish between rotation about X (which changes signs of Y and Z) and reflection in the XZ plane (which changes the sign of Y only).