where ρX
means the
probability of being in form X,
and we have been a little vague about just what we mean by "energy",
since we'll be including "entropy" later.
Although the formulae and models of organic molecules were developed for completely different purposes, they can be useful for estimating molecular energies. Errors in the simplest estimates are given names like, "Strain Energy," which is the main topic in "Conformational Analysis."
Early interest in the energy content of organic substances was due to their use as fuels, particularly as foods. It is not surprising that the first attempt to establish a relationship between energy and molecular structure came from a physiologist (Ludimar Hermann, 1868) and involved the heat of combustion, measured of course by a calorimeter.
Consider why you might expect a relationship between energy content and molecular structure:
Hydrocarbons contain carbon and hydrogen.
Carbon and hydrogen are fuels.
Perhaps the heat liberated in combustion of a hydrocarbon is the sum of the heats from combustion of its carbon and its hydrogen.
So we could see how much heat is liberated by burning a certain mass of graphite, and how much by burning a certain mass of hydrogen gas, and compare with the amount from burning a corresponding amount of various organic compounds. In the following table the compounds with 6 carbon atoms and 12 hydrogen atom are predicted to have a heat of combustion that is 6*(-94.05) + 12*(-57.8/2):
| atoms/mole | atoms/mole | | kcal/mol | kcal/mole | % | |
| |
|
|
|
|
|
|
| | |
| | | |
|
|
| | |
| | |
|
| |
| | |
|
| |
| | |
| | |
|
|
|
| | |
| | |
|
So how good is our "theory"? From the point of view of estimating fuel potential, not so bad for the two hydrocarbons (within 4%). But it is worse for cyclohexanol with one oxygen, and the 36% error for the compound most relevant to physiology, glucose with 6 oxygens, is unacceptable.
There is a much more important reason than fuel potential to predict molecular energies, and it demands much more precise values than the 10 to 250 kcal/mole errors above. The application of statistical analysis to thermodynamics by Maxwell and Boltzmann showed that at a given temperature (T) the probability of a molecule's having a certain amount of energy (E) is proportional to exp(-E/kT), where k is called "Boltzmann's constant".
At equilibrium we can predict the ratio of two different forms of a molecule by knowing their energies. By "different forms" we could mean any sort of difference, for example
The ratio of different forms at equilibrium is called the equilibrium constant. For the equilibrium between A and B:
where ρX
means the
probability of being in form X,
and we have been a little vague about just what we mean by "energy",
since we'll be including "entropy" later.
All we need to know in order to predict the relative amounts of two forms of a substance at equilibrium is their difference in energy, ∆E, and the absolute temperature. For practical purposes at room temperature and with ∆E in kcal/mole one can express the ratio in base 10, rather than base e, as follows:
This relationship may be the most useful thing you will learn in Chem 125. The only challenge is getting the sign right. Here you must use your common sense and be sure to predict predominance of the lower-energy form.
For example if the energy of B is 4 kcal/mole higher than that of A, there should be 103 = 1000 times as much A as B at equilibrium at room temperature.The relationship shows that if we made an error of 4/3 kcal/mole, we would predict a B/A ratio that was wrong by a factor of 10. If we made the smallest error in the table above (12 kcal/mole for ethene), we would be off by a factor of 1,000,000,000. Talk about unacceptable!
We desperately need a scheme for estimating energy that is better than the simple one summarized in the table above, and we would like to be within 1 kcal/mole to predict useful equilibrium constants.
Obviously our scheme for estimating energy content on the basis of carbon and hydrogen content was too na´ve. Cyclohexanol and glucose, the compounds containing oxygen, give off less energy, because they are "part way" to combustion already. One could imagine patching up the theory by subtracting someting for each oxygen in the molecule.
But there is a better way - one that can also help account for the unusually high energy of ethene. This is to assume that the energy of a molecule depends not only on what elements it contains, but also on how they are bonded. In fact this scheme is so good that it is worthwhile to create tables of "Average Bond Energies" (e.g. here).
We are not vitally interested in absolute values of molecular energy, only in differences, since these are what determine equilibrium constants. So we can choose any reference point that we find convenient in defining zero for our scale of energy.
| (I) The most natural choice from the experimental point of view is to compare the energy of organic molecules to that of their products of combustion, CO2, H2O (N2, if there is nitrogen, etc.). Call the energy of CO2, H2O, etc. zero and the energies of a molecule is the measured heat of combustion, as shown in column 5 of the table above and illustrated in the energy diagram at the right for cyclohexane. [Values are reported as negative, since the fuel is higher energy than the products, and the energy of the molecules falls as they release energy on combustion.] One problem with combustion is that the heat evolved is so large that one has to be a very talented and careful experimentalist to measure values accurate to within 1 kcal/mole (0.1%). (II) Another logical choice for zero of our energy scale would be the pure elements (in their standard state) - graphite for carbon, H2 gas at atmospheric pressure for hydrogen, etc. Unfortunately there are no reactions like combustion that would allow measuring the evolution of heat on going directly from the elements to the compound of interest (or vice versa). However, because energy is conserved overall, one has only to measure the heat of combustion of the elements themselves to put the elements on the same scale with the compounds that have been burned. That is, someone must have measured the heat evolved on burning graphite and H2, and you can use their result together with your experimental result for ∆Hcomb of your compound to calculate your "heat of formation" (∆Hf) from the elements. For cyclohexane this value is -29.5 kcal/mole. Cyclohexane is a little more stable than graphite and H2. Ethene is 12.5 kcal/mole less stable than the elements, as shown in the table above. Tables of heats of formation of widely available (e.g. here or more authoritatively from the NIST WebBook). (III) If one wants to estimate molecular energies by summing bond energies, the most natural reference (or zero of the energy scale) is the separated atoms in the gas phase. That is, one would like to have the heat of atomization (∆Hatom) of the compound. If you knew the heat of atomization of the elements in their standard states (e.g. graphite and H2 gas), all you have to do is add, as you can see from the diagram on the right for cyclohexane (-881.6 + 911.1 + 1650.6 = 1680.1) 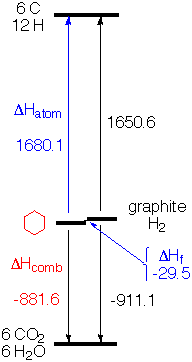 |
If you measure the heat of combustion of your compound (-881.6) and know the heat of combustion of the elements (-911.1), all you need is the heat of atomization of the elements and you can calculate the heat of atomization of your compound. No problem, you just look up the heat of formation (∆Hf) of H atom (52.1 kcal/mole) and that of C is (170.9 kcal/mole). So 6 * C + 12 * H = 1650.6.
Many ∆Hf values are available from spectroscopy. For H2 it was possible to measure the minimum amount of light energy required to make the diatomic molecules dissociate. This was 104.2 kcal/mole, meaning that ∆Hf per H atom is half of this value or 52.1 kcal/mole. One can do the same trick with O2 to find that the ∆Hf of the O atom is 59.6 kcal/mole. But how about the C atom, where the standard state of the element is graphite, not the C2 molecule?
In principle ∆Hf of the carbon atom is available from spectroscopy by measuring the minimum amount of light energy necessary to form a C atom and an O atom from CO. Since we already know ∆Hf of the O atom, and ∆Hf of CO (from its heat of combustion), we should be able to find ∆Hf of the C atom by difference. The apparent value for ∆Hf of the carbon atom was 170.9 kcal/mole.
But originally there was a lot of uncertainty. There was evidence suggesting that the C atom formed by photolyzing CO was not the lowest-energy "ground state" carbon atom with its six electrons in the lowest available orbitals, but an "excited" carbon atom with 30 (or 46) kcal/mole of excess energy, meaning that the true ∆Hf of the carbon atom would be only 141 (or 125) kcal/mole. There were vigorous debates of these and other experimental values involving three future Nobel laureates (Linus Pauling, Robert Mulliken, Gerhard Herzberg) and the "father of the H-bomb" (Edward Teller) as well as many other theoreticians and experimentalists. The 1948 second edition of Pauling's influential Nature of the Chemical Bond chose the value 124.3 kcal/mole.
A discrepancy of 46 kcal/mole is not a small thing. It would make a room temperature equilibrium constant wrong by a factor of 103/4*46 which is about 1033! Fortunately not many people are vitally interested in predicting equilibrium constants involving carbon atoms. The error would just mean that bond strengths involving carbon would be wrong, but calculated differences between molecules whose equilibrium is of interest might still be correct. [This is one manifestation of a general principle that numbers that are really important are usually relatively easy to determine, because their influence makes precise measurement possible.]
| In principle there was a non-spectroscopic method for measuring ∆Hf of the C atom that could settle the debate. It involved measuring the vapor pressure of C atoms in equilibrium with graphite at a given temperature, or the variation of this pressure with temperature. Usually we want to know energy differences to predict equilibrium constants, but it is possible to run the Boltzmann equation "backwards" to determine an energy difference from a measured equilibrium constant. If [B] and [A] in the equation above are replaced by the pressure of C-atoms (or a quantity proportional to this pressure) and by solid graphite, respectively, then a constant b (involving the proportionality constant and "entropy" and the constant "concentration" of graphite) is introduced into the equation to give the first equation on the right, where PC is the pressure of C-atoms and ∆HfC is the heat of atomization of graphite or the heat of formation of the carbon atom. Taking logs gives the second equation, which says that plotting the log of the pressure of carbon atoms against 1/T will give a straight line whose slope is -∆HfC/R. So you just multiply the slope by -R to get the heat of formation of gaseous C-atoms from graphite. | |
| |
So "all" someone had to do was to measure the vapor pressure of carbon atoms in equilibrium with graphite over a range of temperatures. One problem is that the pressure is vanishingly small except at fabulously high temperature (even at 2400K the vapor pressure of C1 is less that 10-7 atmospheres). A second problem is that other species, like C2, C3, and other aggregates of carbon contribute to the tiny vapor pressure over very hot graphite.
|
Shortly after finishing graduate school in 1951, William Chupka, an instructor at Harvard (and subsequently a professor of chemistry at Yale), took on this challenge. He decided to solve the second problem by using a mass spectrometer, which measures the concentration of gas phase ions after separating them by mass. All he would have to do is to bombard the equilibrium gas with high-energy electrons to knock out other electrons and generate positive ions, and he could measure the amount of C+ as a measure of the amount of C in the original gas. |
|
Now Chupka had to figure out how to introduce the equilibrium gas at known temperatures greater than 2000 K into a mass spectrometer. With a collaborator named Mark Inghram he designed and constructed the evacuated apparatus shown at the right, which attached onto a mass spectrometer at the top. In the center was an oven about 3 cm high (E, red) with a graphite liner (black). The oven was made of tantalum, the only element with a higher heat of vaporization than carbon's. The oven was surrounded by several rings of tungsten wire (B, violet), which was heated by an electrical current until it began to boil off electrons. The tantalum oven was kept 500 to 1000 volts more positive that the wire (which of course it did not touch), so the electrons would slam into the oven and deposit enough energy to heat it, and its graphite liner, to temperatures from 2100 to 2400 K. The nested tantalum liners (C) around the oven served as a shield to prevent it from losing too much heat by radiation. [For reference, the temperature of a typical gas/air flame is 2200 K. Tantalum melts at 3293 K. Normal glass softens at about 800 K, and quartz glass at about 1700 K.] The space within the red oven thus contained gases (C1, C2, C3, etc.) which are supposed to be at equilibrium with the graphite liner. A tiny hole in the top of the oven allowed the gases to leak out very slowly into the evacuated surroundings (red arrow). The hole was small enough (less that 1/1500 of the surface area of the graphite) that the loss of gases would not appreciably disturb the equilibrium within the oven. In the space G the emerging gases were struck by an electron beam (I) to knock out electrons and convert them to ions, which were then separated and measured individually by the mass spectrometer. The intensity of the C+ signal (times the temperature, hot atoms move faster and generate more pressure) was proportional to the pressure of C1 within the oven. Of course Chupka had to know the temperature, as well as the pressure of C atoms. He achieved this by drilling a small hole in the radiation shield so that one could see the oven through a quartz window F (along the red line). He used a high melting quartz window because a normal glass window would have softened from the high temperature. Observing the light emitted by the glowing oven with a "pyrometer" allowed measuring its temperature to within 30░. Although we use red to denote that the oven is hot, and black to denote graphite, the actual color of oven and graphite at 2400 K is the orange of the operating filament of a 60W lightbulb. After performing a lot of calibration and controls, Chupka was able to make a plot of the log of the pressure of C1 (and of other species) against 1/T, to get a straight line as described by the equation above. Note that the bottom axis is in fact 10,000/T and the vertical axis is the log of a quantity proportional to pressure (intensity of the ion beam times temperature). The slope of this line confirmed the spectroscopic value of 170.9 kcal/mole as the correct heat of atomization of graphite. When the Chupka-Inghram experiment was published in 1955, the Nobel Prize winners stopped arguing about the heat of atomization of carbon, and the world of science accepted this value. In the 3rd edition of The Nature of the Chemical Bond (1960) Pauling gave a value of 171.70 kcal/mole. The currrent value reported by the National Institute of Standards and Technology is 171.29(▒ 0.11) Chupka was right on. | |
| |
The following table compares heats of atomization calculated by summing average bond energies with the experimental values from heats of combustion of the compounds and heats of atomization of the elements:
| | Energies | | kcal/mol | % | |||||
| | |||||||||
| | |||||||||
| | |||||||||
| | |||||||||
| |
Contrast these errors of 4-16 kcal/mole (<1%) with the 10-241 kcal/mole errors in the first crude model at the beginning of this discussion, where we considered only what atoms are involved, not how they are bonded. Things are getting much better. [Most of the error for α-glucose comes because it is burned as a solid, which is already lower in energy than the gas would be.]
An error of 4 kcal/mole out of 538 is quite impressive with respect to how well the model functions, but for practical purposes of estimating an equilibrium constant or a reaction rate it is still unacceptable. Such predictions would be in error by a factor of 10-3/4 * 4 = 1000. We would like to be within a factor of 10, which would correspond to an error of 4/3 = 1.3 kcal/mole.
We need a more elaborate scheme for estimating molecular energies. Enter "Strain Energy."
| |